《Mahout in Action》一书中提到,归一化可以略微提高准确性。能否有人解释一下原因,谢谢!
回答:
归一化并非总是必要的,但它很少会造成损害。
一些例子:
K-means聚类在空间的所有方向上都是“各向同性”的,因此倾向于产生或多或少是圆形(而不是细长)的聚类。在这种情况下,保持方差不等价于对方差较小的变量赋予更大的权重。
Matlab中的示例:
X = [randn(100,2)+ones(100,2);... randn(100,2)-ones(100,2)];% 引入去归一化% X(:, 2) = X(:, 2) * 1000 + 500;opts = statset('Display','final');[idx,ctrs] = kmeans(X,2,... 'Distance','city',... 'Replicates',5,... 'Options',opts);plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12)hold onplot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12)plot(ctrs(:,1),ctrs(:,2),'kx',... 'MarkerSize',12,'LineWidth',2)plot(ctrs(:,1),ctrs(:,2),'ko',... 'MarkerSize',12,'LineWidth',2)legend('Cluster 1','Cluster 2','Centroids',... 'Location','NW')title('K-means with normalization')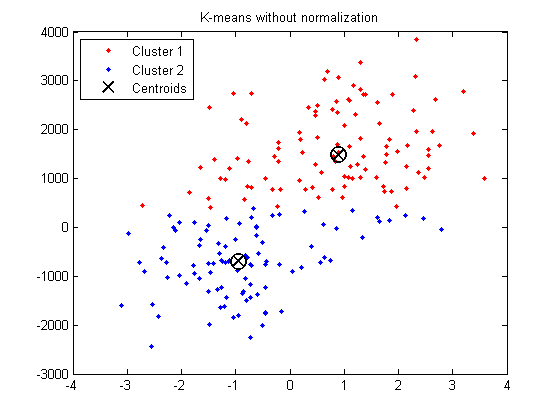
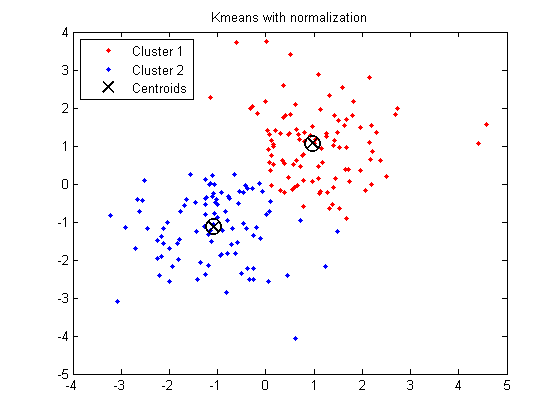
(仅供参考:如何检测我的数据集是否聚类或未聚类(即形成单一聚类))
比较分析显示,分布式聚类结果取决于归一化程序的类型。
如果输入变量是线性组合的,如在MLP中,那么理论上至少很少需要标准化输入。其原因是任何输入向量的重新缩放都可以通过改变相应的权重和偏置来有效地撤销,从而使您得到与之前相同的输出。然而,出于各种实际原因,标准化输入可以使训练更快,并减少陷入局部最优的几率。此外,使用标准化输入可以更方便地进行权重衰减和贝叶斯估计。
您应该对数据进行这些操作吗?答案是,这取决于情况。
标准化输入或目标变量往往能使训练过程表现得更好,通过改善优化问题的数值条件(参见ftp://ftp.sas.com/pub/neural/illcond/illcond.html)并确保涉及初始值和终止的各种默认值适当。标准化目标还可以影响目标函数。
对案例进行标准化应谨慎处理,因为它会丢弃信息。如果这些信息无关紧要,那么标准化案例可能非常有帮助。如果这些信息很重要,那么标准化案例可能会带来灾难性的后果。
有趣的是,改变测量单位甚至可能导致人们看到非常不同的聚类结构:Kaufman, Leonard, 和 Peter J. Rousseeuw.. “Finding groups in data: An introduction to cluster analysis.” (2005).
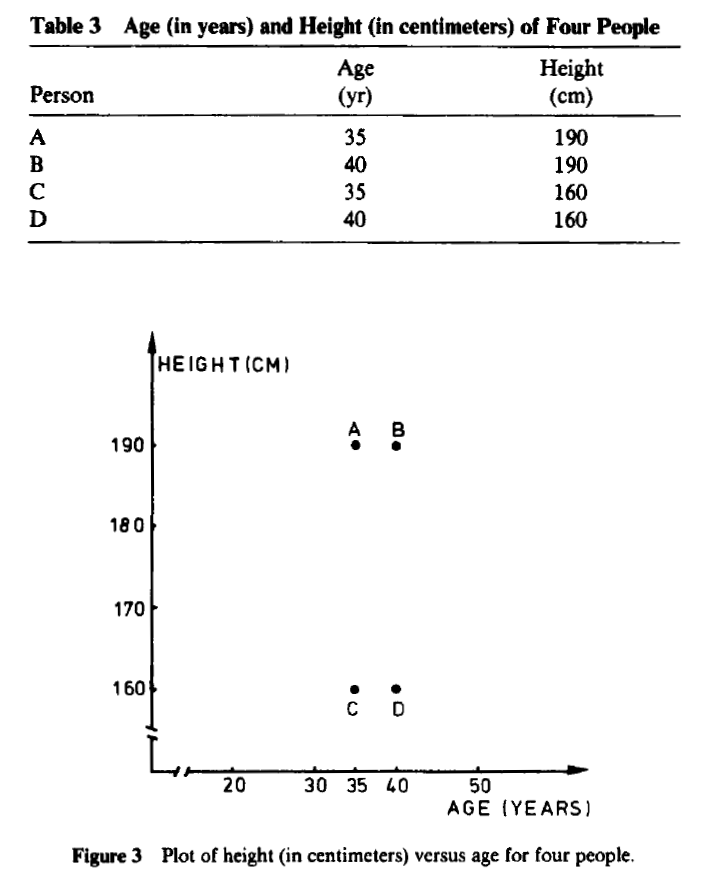
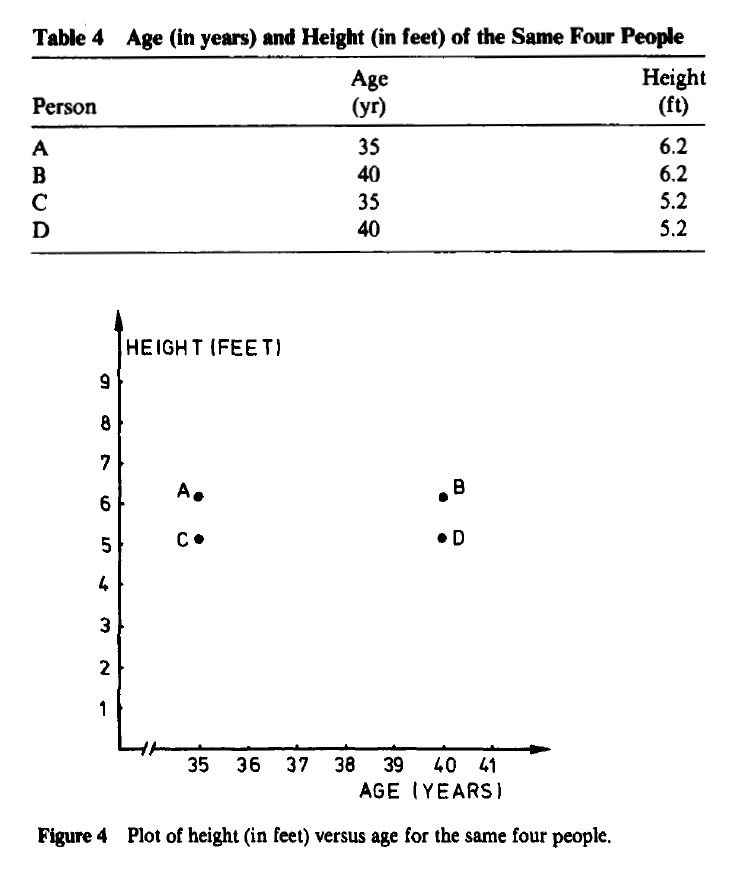
在某些应用中,改变测量单位甚至可能导致人们看到非常不同的聚类结构。例如,四个虚构人的年龄(以年为单位)和身高(以厘米为单位)在表3中给出,并在图3中绘制。看起来{A, B}和{C, D}是两个明显分离的聚类。另一方面,当身高以英尺表示时,得到表4和图4,其中明显的聚类现在是{A, C}和{B, D}。这种划分与第一个完全不同,因为每个对象都获得了另一个同伴。(如果年龄以天为单位测量,图4会变得更加扁平。)
为了避免这种对测量单位选择的依赖性,可以选择标准化数据。这将原始测量转换为无单位的变量。
Kaufman等人继续提出了一些有趣的考虑(第11页):
从哲学的角度来看,标准化并没有真正解决问题。实际上,测量单位的选择引起了变量的相对权重。用较小的单位表达一个变量会导致该变量的范围变大,从而对结果结构产生较大的影响。另一方面,通过标准化,人们试图给所有变量赋予相同的权重,希望达到客观性。因此,它可能被没有先验知识的从业者使用。然而,在特定应用中,某些变量可能本质上比其他变量更重要,那么权重的分配应该基于主题知识(例如,Abrahamowicz, 1985)。另一方面,已经尝试设计出与变量规模无关的聚类技术(Friedman和Rubin, 1967)。Hardy和Rasson(1982)的提议是寻找一个最小化聚类凸包总体积的划分。原则上,这种方法对于数据的线性变换是不变的,但遗憾的是目前没有实现它的算法(除了一个仅限于二维的近似)。因此,目前标准化的困境似乎是不可避免的,本文描述的程序将选择权留给用户。