我有以下代码,主要尝试使用randomForest从iris数据中预测Species。我真正感兴趣的是找到最能解释物种分类的最佳特征(变量)。我发现randomForestExplainer包最适合此目的。
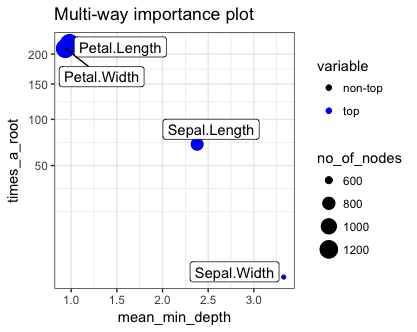
library(randomForest)library(randomForestExplainer)forest <- randomForest::randomForest(Species ~ ., data = iris, localImp = TRUE)importance_frame <- randomForestExplainer::measure_importance(forest)randomForestExplainer::plot_multi_way_importance(importance_frame, size_measure = "no_of_nodes")代码的结果产生了以下图表:
根据图表,解释为什么Petal.Length和Petal.Width是最佳因素的关键因素如下(解释基于vignette):
mean_min_depth– 通过参数mean_sample指定的三种方式之一计算的平均最小深度,times_a_root– 在Xj被用于分割根节点的树的总数(即,根据Xj的值将整个样本分成两部分),no_of_nodes– 使用Xj进行分割的节点总数(如果树较浅,通常等于no_of_trees),
我不是很清楚为什么高times_a_root和no_of_nodes更好?而低mean_min_depth更好?
这些有什么直观的解释吗?
vignette的信息没有帮助。
回答:
你希望统计模型或度量在“能力”和“简洁性”之间取得平衡。randomForest在内部设计时采用了惩罚策略,以实现简洁性。此外,在任何给定样本中选择的变量数量将少于预测变量的总数。这允许在数据集中预测变量的数量超过样本(行)数量时进行模型构建。早期的分割或分类规则可以相对容易地应用,但后续的分割变得越来越难以满足有效性标准。“能力”是正确分类不在子样本中的项目的能力,为此使用了一个代理,即所谓的OOB或“袋外”项目。randomForest的策略是多次进行这种操作,以建立一组代表性的规则,这些规则在假设袋外样本将公平地代表产生整个数据集的“宇宙”的情况下对项目进行分类。
times_a_root属于测量变量相对于其“竞争者”的“相对能力”的类别。times_a_root统计量测量变量在决策树“顶部”的次数,即在选择分割标准的过程中被首先选择的可能性。no_of_node测量变量在所有子样本中被选择作为分割标准的总次数。从:
?randomForest # 查找对象leavesforest$ntree[1] 500的名称… 我们可以看到用于评估图表y轴上大约200值的分母。大约2/5的样本回归将Petal.Length作为顶级分割标准,而另外2/5将Petal.Width作为最重要的变量选择为顶级变量。大约500个中有75个有Sepal.Length,而只有大约8或9个有Sepal.Width(… 这是对数尺度。)在iris数据集的情况下,子样本将忽略每个子样本中的至少一个变量,因此times_a_root的最大可能值将小于500。在这种情况下,200的得分相当不错,我们可以看到这两个变量具有可 compar的解释能力。
no_of_nodes统计量总计了具有该变量的树的总数,记住节点数量将受到惩罚规则的约束。