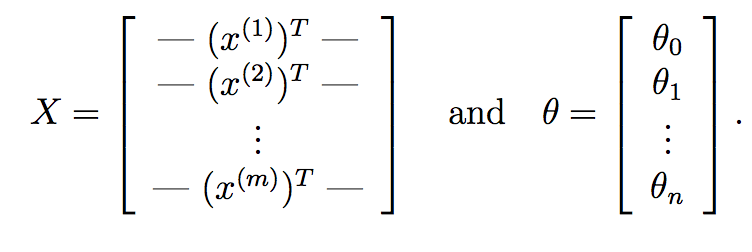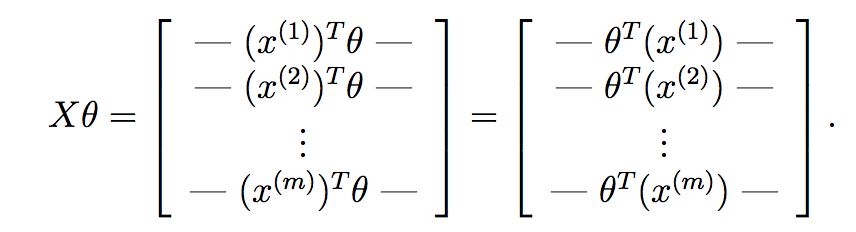我正在尝试在一个具有单一特征和多个训练样本(m)的数据集上实现批量梯度下降。
当我尝试使用正常方程时,我得到了正确的答案,但使用下面的MATLAB代码执行批量梯度下降时却得到了错误的答案。
function [theta] = gradientDescent(X, y, theta, alpha, iterations) m = length(y); delta=zeros(2,1); for iter =1:1:iterations for i=1:1:m delta(1,1)= delta(1,1)+( X(i,:)*theta - y(i,1)) ; delta(2,1)=delta(2,1)+ (( X(i,:)*theta - y(i,1))*X(i,2)) ; end theta= theta-( delta*(alpha/m) ); computeCost(X,y,theta) endendy 是目标值的向量,X 是一个矩阵,其第一列全是1,第二列是值(变量)。
我已经使用向量化实现了这个方法,即
theta = theta - (alpha/m)*delta… 其中 delta 是一个初始化为零的2元素列向量。
成本函数 J(Theta) 是 1/(2m)*(sum from i=1 to m [(h(theta)-y)^2])。
回答:
错误非常简单。你的 delta 声明应该在第一个 for 循环内部。每次你累积训练样本和输出之间的加权差异时,你都应该从头开始累积。
如果你不这样做,你所做的就是累积来自前一次迭代的错误,这会将之前学习的 theta 版本的错误考虑在内,这是不正确的。你必须将这放在第一个 for 循环的开头。
此外,你似乎有一个多余的 computeCost 调用。我假设这是在每次迭代时根据当前参数计算成本函数,因此我将创建一个名为 cost 的新输出数组,在每次迭代时显示这个值。我还将调用这个函数并将其分配给数组中的相应元素:
function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations) m = length(y); costs = zeros(m,1); %// 新增% delta=zeros(2,1); %// 删除 for iter =1:1:iterations delta=zeros(2,1); %// 放置在这里 for i=1:1:m delta(1,1)= delta(1,1)+( X(i,:)*theta - y(i,1)) ; delta(2,1)=delta(2,1)+ (( X(i,:)*theta - y(i,1))*X(i,2)) ; end theta= theta-( delta*(alpha/m) ); costs(iter) = computeCost(X,y,theta); %// 新增endend关于正确向量化的说明
顺便说一句,我不认为这个实现是完全向量化的。你可以通过使用向量化操作来消除第二个 for 循环。在我们这样做之前,让我先讲一些理论,以便我们达成共识。你在这里使用的是线性回归中的梯度下降。我们希望寻找最佳参数 theta,这些是我们的线性回归系数,旨在最小化这个成本函数:
m 对应我们可用的训练样本数量,x^{i} 对应第 i 个训练样本。 y^{i} 对应与第 i 个训练样本相关联的真实值。 h 是我们的假设,它被定义为:
请注意,在2D线性回归的上下文中,我们只需要计算 theta 中的两个值 – 截距项和斜率。
我们可以通过最小化成本函数 J 来确定最佳回归系数,这些系数可以为我们提供最佳预测,从而最小化训练集的误差。具体来说,从一些初始的 theta 参数开始…通常是一个零向量,我们从1迭代到我们认为合适的次数,在每次迭代中,我们通过以下关系更新我们的 theta 参数:
对于我们想要更新的每个参数,你需要确定成本函数相对于每个变量的梯度,并在当前 theta 状态下评估它是什么。如果你用微积分计算出来,我们得到:
如果你不清楚这个推导是如何发生的,那么我建议你参考这个很好的数学堆栈交换帖子,它讨论了这个问题:
现在…我们如何将这个应用到我们当前的问题中?具体来说,你可以很容易地分析所有样本并一次性计算 delta 的条目。我的意思是,你可以这样做:
function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations) m = length(y); costs = zeros(m,1); for iter = 1 : iterations delta1 = theta(1) - (alpha/m)*(sum((theta(1)*X(:,1) + theta(2)*X(:,2) - y).*X(:,1))); delta2 = theta(2) - (alpha/m)*(sum((theta(1)*X(:,1) + theta(2)*X(:,2) - y).*X(:,2))); theta = [delta1; delta2]; costs(iter) = computeCost(X,y,theta); endend对 delta(1) 和 delta(2) 的操作可以完全向量化在一个语句中对两者进行。你所做的就是对每个样本 i 从 1, 2, ..., m 计算 theta^{T}*X^{i}。你可以方便地将这个放入一个 sum 语句中。
我们可以进一步将其替换为纯粹的矩阵操作。首先,你可以使用矩阵乘法非常快速地计算每个输入样本 X^{i} 的 theta^{T}*X^{i}。假设如果:
这里,X 是我们的数据矩阵,它由对应 m 个训练样本的 m 行和对应 n 个特征的 n 列组成。同样,theta 是我们从梯度下降中学习的权重向量,具有 n+1 个特征,考虑了截距项。
如果我们计算 X*theta,我们得到:
如你所见,我们已经为每个样本计算了假设,并将每个假设放入一个向量中。这个向量的每个元素是第 i 个训练样本的假设。现在,回想一下梯度下降中每个参数的梯度项是什么:
我们希望一次性为你学习向量中的所有参数实现这个,因此将其放入一个向量中,我们得到:
最后:
因此,我们知道 y 已经是一个长度为 m 的向量,因此我们可以通过以下方式非常紧凑地计算每次迭代的梯度下降:
theta = theta - (alpha/m)*X'*(X*theta - y);… 所以你的代码现在只是:
function [theta, costs] = gradientDescent(X, y, theta, alpha, iterations) m = length(y); costs = zeros(m, 1); for iter = 1 : iterations theta = theta - (alpha/m)*X'*(X*theta - y); costs(iter) = computeCost(X,y,theta); endend