我目前在研究神经网络理论,我发现到处都写着它包括以下几层:
- 输入层
- 隐藏层
- 输出层
我看到一些图形描述将输入层展示为网络中的真实节点,而另一些则展示为仅是数值向量 [x1, x2, … xn]
正确的结构是什么?
“输入层”是一个真实的神经元层吗?还是只是抽象地命名为层,而实际上只是输入向量?
我添加了一些我在网上找到的矛盾且令人困惑的图片:
这里看起来输入层由神经元组成:
这里看起来输入层只是一个输入向量: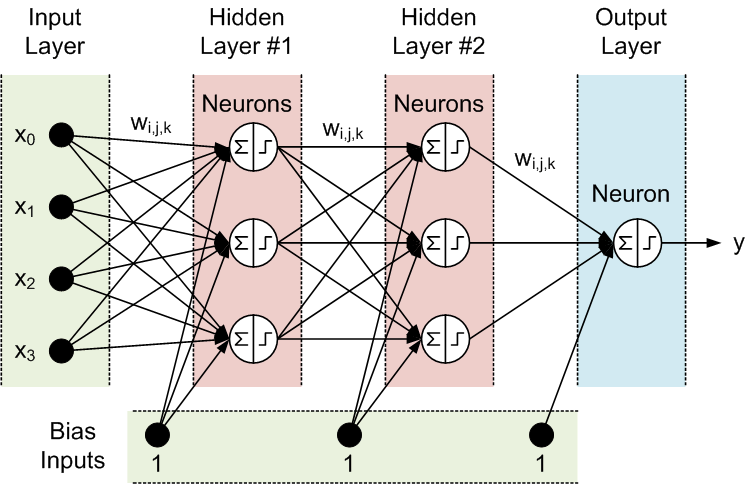
回答:
让我用一些数学符号来回答你的问题,这样比随机图片更容易理解。首先,回顾一下感知器。
感知器的任务是找到一个决策函数,将给定集合中的某些点分类到n个类别中。因此,对于一个函数
f : R^n -> R , f(X) = <W, X> + b其中W是权重向量,X是点向量。例如,如果你有一条由方程 3x + y = 0 定义的线,那么W是 (3,1),X是 (x,y)。
神经网络可以被视为一个图,其中图的每个顶点都是一个简单的感知器——也就是说,网络中的每个节点仅仅是一个接受某些值并输出一个新值的函数,这个新值可以用于下一个节点。在你的第二张图片中,这将是两个隐藏层。
那么这些节点需要什么作为输入呢?一组W和Xs——权重和点向量。在你的图片中,这由 x0, x1, .. xn 和 w0, w1, .. wn 表示。
最终,我们可以得出结论,神经网络需要运行的一组输入向量是权重和点。
我对你的总体建议是,选择一个学习来源并坚持下去,而不是在网上浏览那些相互矛盾的图片。